상관계수는 통계학에서 두 변수 간의 선형관계의 강도와 방향을 나타내는 지표입니다. 이번 포스팅에서는 상관계수의 의미와 계산방법, 활용할 수 있는 분야까지 알아보도록 하겠습니다.
1. 상관계수(correlation coefficient)의 의미
상관계수는 통계학에서 두 변수 간의 선형 관계의 강도와 방향을 측정하는 지표입니다. 상관계수는 -1부터 1까지의 범위를 가지며, 0에 가까울수록 두 변수 간의 선형 관계가 약하고, 1 또는 -1에 가까울수록 선형 관계가 강하다는 의미를 가지게 됩니다.
상관계수 값의 해석은 아래와 같이 합니다.
* 1에 가까울수록 양의 선형 관계가 강합니다.
* 0에 가까울수록 두 변수 사이의 선형 관계가 약합니다.
*-1에 가까울수록 음의 선형 관계가 강합니다.
아래 그림을 참고하면 이해가 쉬울 것입니다.
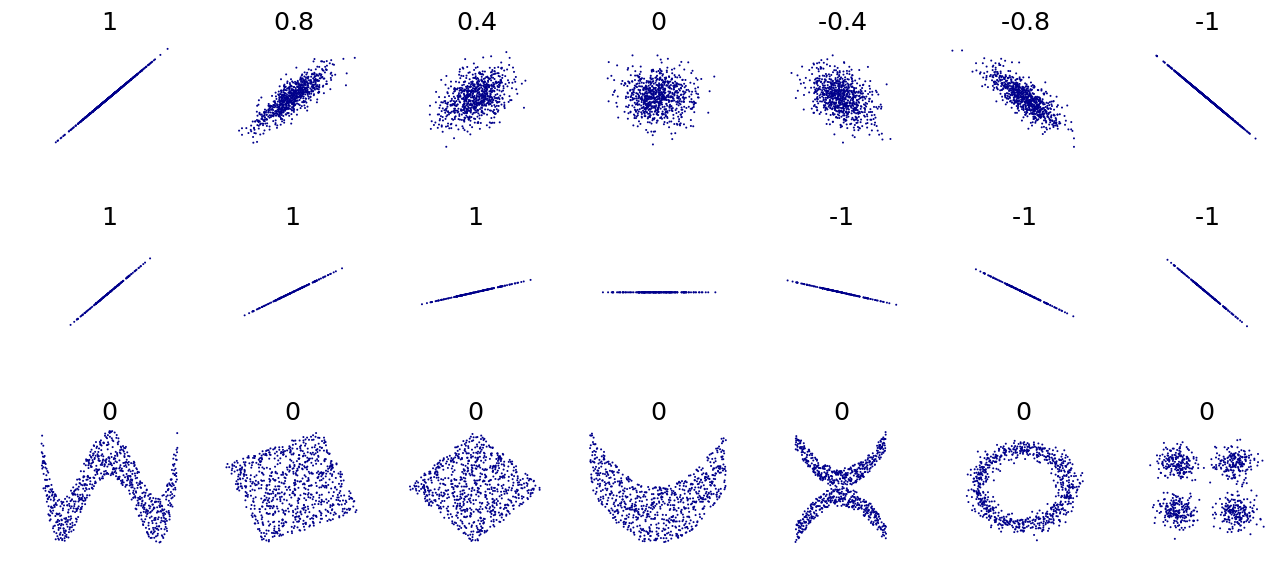
2. 상관계수 계산법
상관계수 중 가장 흔하게 사용하는 피어슨 상관계수(Pearson correlation coefficient)의 계산방법에 대해 살펴보겠습니다.
참고로 피어슨 상관계수의 '피어슨'은 통계학자 칼 피어슨(Karl Pearson)의 이름을 따서 지어졌습니다. 칼 피어슨은 19세기와 20세기 초반에 활동한 영국의 통계학자로 다양한 통계적 개념과 방법을 개발하고, 통계학의 발전에 큰 기여를 했습니다.
피어슨상관계수는 두 변수 X와 Y의 공분산을 각각의 표준편차의 곱으로 나누어 계산합니다.

여기서 Σ는 합을 나타내고, X와 Y는 각각의 변수 값, 평균(X)과 평균(Y)는 X와 Y의 평균값, n은 데이터 쌍의 개수입니다.
이렇게 계산된 피어슨 상관계수는 -1부터 1까지의 범위를 가지며, -1은 완전한 음의 상관관계, 1은 완전한 양의 상관관계, 0은 상관관계가 없음을 나타냅니다.
3. 상관계수 활용 분야
1. 금융 분야: 주식 시장에서 두 주식의 수익률 간의 상관계수를 분석하여, 두 주식이 얼마나 관련성이 있는지 파악할 수 있습니다. 이를 통해 투자리스크를 관리하고 포트폴리오의 다변화를 구성하는데 활용 가능합니다.
2. 마케팅 분야: 광고 비용과 판매량 사이의 상관계수를 분석하여, 광고 효과를 평가하거나 마케팅 전략을 기획할 수 있습니다. 또한 소비자 행동과 제품 특성 간의 관련성을 파악하여 상품의 타깃 시장을 정확히 파악할 수 있습니다.
3. 의학 분야: 약물의 효과와 부작용 사이의 관련성을 상관계수를 통해 분석할 수 있습니다. 또한, 건강 지표 간의 상관계수를 분석하여 질병 발생과의 관련성을 파악하고 예방에 도움을 줄 수 있습니다. 예를 들어 비만지수와 혈압 수치의 상관관계 등을 분석할 수 있습니다.
4. 사회과학 분야: 교육 수준과 소득 수준, 범죄율과 경제 성장률 등 사회 현상 간의 상관계수를 분석하여 사회 문제를 이해하고 정책 결정에 활용할 수 있습니다.
4. (참고) 결정계수(R-squared)란?
나중에 회귀분석을 다룰 포스팅에서 자세히 설명하겠지만 상관계수와 결정계수는 관계가 있기 때문에 여기서도 살짝 언급하고자 합니다.
결정계수(R-squared)는 회귀분석 모델이 종속 변수의 변동을 얼마나 잘 설명하는지를 나타내는 지표입니다. 0과 1 사이의 값을 가지며, 1에 가까울수록 모델이 데이터를 잘 설명한다는 의미입니다.
결정계수가 0.8이라면, 회귀 모델이 데이터의 80%를 설명한다는 것을 의미합니다.
결정계수는 상관계수의 제곱과 동일한 값으로 계산됩니다. 따라서, 상관계수가 높을수록 (절댓값이 1에 가까울수록) 결정계수 역시 높아지며, 두 변수 간의 관계를 더 잘 설명하는 모델이라고 할 수 있습니다.
'통계학 용어' 카테고리의 다른 글
| 통계적 검정 방법- 가설 검정이란? (0) | 2023.10.13 |
|---|---|
| 자유도- 샘플의 표준편차는 왜 n-1로 나눌까 (0) | 2023.10.13 |
| 샘플을 추출하는 여러가지 방법(샘플링, sampling) (0) | 2023.10.12 |
| 모집단과 모집단을 대표하는 샘플, 샘플링편향 (1) | 2023.10.11 |
| 데이터의 분포와 변동성- 평균, 분산, 표준편차 (0) | 2023.10.10 |